Hablar del perímetro de un rectángulo parece elemental, pero dominarlo evita errores al comprar malla para cercas, cotizar marcos o programar interfaces. Así pues, este es la medida del contorno de una figura plana, tratándose del contorno de una figura y la medida de ese contorno. En un rectángulo, como hay 2 lados de una medida y otros 2 de otra, la suma de sus 4 lados puede reagruparse y escribirse de manera compacta, razón por la que la fórmula práctica no es más que una abreviación del proceso de sumar lado a lado.
Fórmula del perímetro de un rectángulo
Es recomendable comenzar sumando cada lado y luego consolidar una expresión breve que haga visible la estructura de la figura. Esa transición evita memorizar fórmulas sin comprender y conecta el tema con situaciones reales: cuánto alambre necesitas para bordear un jardín o cuánta moldura comprar para una puerta.
La regla es directa: P = 2L + 2A, donde L es el largo y A el ancho, de manera que, tras practicar la suma de cada lado, el estudiantado pueda expresar de manera sintética ese procedimiento como 2a + 2b y, finalmente, P = 2a + 2b.
Esta es una presentación que deja claro que el perímetro de un rectángulo se obtiene sumando todas las longitudes del contorno y que la fórmula solamente comprime esa suma en una expresión equivalente.
De tal manera, un rectángulo tiene 2 lados de longitud L y 2 de longitud A. Si escribes la suma como L + A + L + A y agrupas términos iguales, obtienes (L + L) + (A + A) = 2L + 2A. La identidad es válida con unidades (m, cm, km), siempre que mantengas la consistencia antes de sustituir valores. Si trabajas con decimales, conviene redondear solamente al final para no arrastrar variaciones.
Explicar explícitamente qué área y perímetro de un rectángulo son magnitudes distintas reduce confusiones, mientras que, el perímetro y el área de una figura son magnitudes independientes.
Así pues, cuando el alumnado compara pares de figuras con igual área, pero contornos distintos, comprende que el contorno no depende de la superficie.
De tal manera, al resolver problemas, acompaña cada cálculo con un dibujo sencillo y señala los lados que estás sumando.
¿Cuál es la diferencia entre perímetro y área?
La diferencia entre perímetro y área es que el perímetro de un rectángulo se trata de la longitud del contorno (suma de lados). Su resultado es en unidades lineales (m, cm). Por su parte, el área es la medida de la superficie encerrada. Resultado en unidades cuadradas (m², cm²).
Estas son magnitudes independientes con 2 figuras pueden tener la misma área y distinto contorno, o al revés, tratándose de una aclaración que elimina la confusión frecuente de creer que, si 2 figuras “se ven parecidas”, tendrán la misma medida perimetral. En realidad, pequeñas variaciones en un lado cambian el contorno sin alterar necesariamente la superficie.
Un error habitual en secundaria y bachillerato es mezclar unidades: reportar el perímetro en m² o el área en metros lineales.
De tal manera, la regla de oro es sencilla; si sumas lados, usas unidades lineales; si multiplicas dimensiones para cubrir superficie, usas unidades cuadradas. Es una buena práctica escribir las unidades en cada línea de cálculo.
Ejemplos resueltos del perímetro de un rectángulo
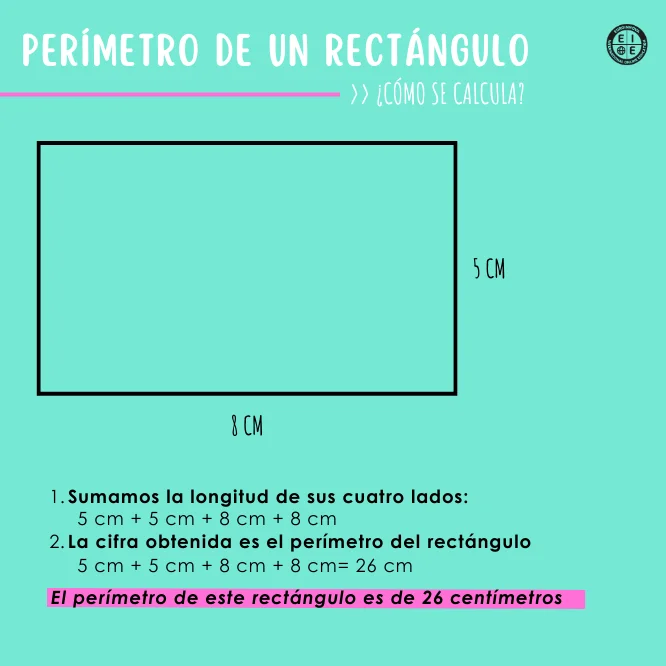
Ejemplo 1 → lados enteros (L=8 cm, A=5 cm)
P = 2L + 2A = 2·8 + 2·5 = 16 + 10 = 26 cm.
Con una tira de 26 cm rodeas el rectángulo por completo. Si en la tienda venden rollos de 10 cm, debes comprar 3 rollos; te sobrarán 4 cm.
Ejemplo 2 → lados con decimales (L=12.5 m, A=7.3 m)
P = 2·12.5 + 2·7.3 = 25.0 + 14.6 = 39.6 m.
Al trabajar con decimales, evita redondear 12.5 a 13 o 7.3 a 7 antes del cálculo. El redondeo final (39.6 m → 39.60 m) es suficiente para reportes técnicos.
Ejemplo 3 → aplicado a un terreno o jardín
Un lote rectángulo de 20.4 m por 12.8 m requiere malla perimetral de P = 2·20.4 + 2·12.8 = 40.8 + 25.6 = 66.4 m.
De este modo, añade 3–5 % extra por traslapes y desperdicio, lo cual constituye un criterio habitual de compra en ferretería.
Aplicaciones del perímetro de un rectángulo
Las aplicaciones del perímetro de un rectángulo son las siguientes:
En construcción
- Cercado y obra negra: el contorno de un claro rectangular determina la cantidad de malla, alambre recocido, molduras y zoclos.
- Carpintería y aluminio: los marcos de puertas y ventanas se cotizan por longitud total, de modo que, medir mal el contorno, aumenta el costo por recorte o rehacer pieza.
- Instalaciones: registros, tapas y ductos suelen modelarse con plantas rectangulares. Su contorno guía cintas, aislantes y selladores.
En diseño gráfico o impresión
- Sangrados y marcos: conocer el contorno del pliego ayuda a definir filetes, márgenes y reglas de corte consistentes.
- Rotulación y etiquetas: el vinil perimetral de un cartel se calcula por la longitud total del borde; no lo confundas con el área de impresión, que sirve para costear tinta/material.
En programación y geometría computacional
- Colisiones (“hitboxes”): aunque el área importa para físicas, usar el contorno del sprite rectángulo mejora la detección de bordes.
- Visión por computadora: al detectar objetos, es común encerrar la región en una “caja delimitadora” (rectángulo) y derivar su contorno para métricas de forma.
- CAD/CAM: las trayectorias de corte siguen contornos paramétricos; P ayuda a estimar tiempo de máquina y longitud de herramienta activa.
Consejos de verificación rápida en ejercicios
- Dibuja y etiqueta: marca L y A; si el dibujo contradice los datos, tales como, por ejemplo, A>L, pero lo representas al revés, es fácil equivocarse al sustituir.
- Estimación previa: si L y A valen decenas, espera un perímetro en decenas también. Si obtienes una cifra minúscula, revisa unidades.
- Prueba con casos extremos: si A→0, el rectángulo se aproxima a un segmento y P→2L; la fórmula P=2L+2A respeta ese límite.
- Revisa unidades: línea por línea; escribe m, cm o km para “ver” si estás sumando longitudes o áreas.
- Orden de operaciones: multiplica antes de sumar (2L + 2A), no al revés; evita sumar L + A y luego duplicar solamente una vez.
¿Qué pasa si sólo conozco el perímetro y un lado?
Puedes despejar. Si P = 2L + 2A y conoces L y P, entonces A = (P − 2L)/2. Si conoces A y P, despeja L = (P − 2A)/2.
Estos despejes son útiles para recuperar dimensiones faltantes a partir de la medición del contorno real, como en terrenos donde mides la cerca y una sola fachada.
Si además conoces el área S, recuerda que S = L·A: resolverías un sistema con 2 ecuaciones para encontrar L y A.
Errores frecuentes y cómo evitarlos
Comprender y aplicar el perímetro del rectángulo es un conocimiento que trasciende el aula y se convierte en un recurso útil para la vida diaria y profesional.
Algunos errores frecuentes son los siguientes:
- Confundir contorno con superficie: lo solucionas releyendo la pregunta y subrayando si pide perímetro o área.
- Mezclar centímetros con metros: convierte todo a una sola unidad antes de operar.
- Olvidar duplicar ambos lados: escribir sólo 2L + A produce un contorno menor al real. Verifica que hayas sumado las 4 longitudes.
- Redondear demasiado pronto: conserva más decimales durante el cálculo y redondea al reportar.
El perímetro de un rectángulo como herramienta matemática y práctica
Dominar el perímetro de un rectángulo ahorra dinero y retrabajos en dimensiones cercas, marcos y trayectorias con precisión, así como programas con menos fallos cuando representas contornos.
Así pues, desde calcular la cantidad de material necesario para cercar un terreno hasta planificar el marco de una construcción, dominar esta fórmula permite resolver problemas reales de manera sencilla y eficiente.
Quizá te interesa leer sobre: